Skip to main content

Neural Octahedral Field

These are old results from a previous preprint, but the overall concept remains valid.

Preprint
Code

WARNING This page will allocate many WebGL contexts.

Motivation​

Since the badge generation project, I have been captivated by quad meshing. The edge-loop centered operations enable concise and fine-grained control, which are hard to replicate with other geometry representations (i.e. the implicit one).

To bridge the gap, I started with the common practice of extracting mesh then quadrilateral remeshing pipeline. After scrutinizing the source code of Instant meshes, I was drawn by its guiding cross field, which automatically snaps to sharp features under sufficient smoothness in 3D ambient space. Though it is only defined in 2-manifold and measuring its smoothness requires pairwise matching, the local smoothing alone immediately strikes me as a possible lead for neural implicit representation. Following this path, I later came across its 3D generalization, the octahedral field, that under its Spherical Harmonics (SH) parameterized functional representation, ticks all the boxes:

  • Well defined in Euclidean space
  • Matching-free smoothing*
  • Snaps to sharp features under sufficient smoothness*

making it the perfect candidate for implicit integration

Overview​

Given a uniformly sampled oriented point cloud, we leverage MLPs to jointly fit the implicit SDF and the octahedral field.

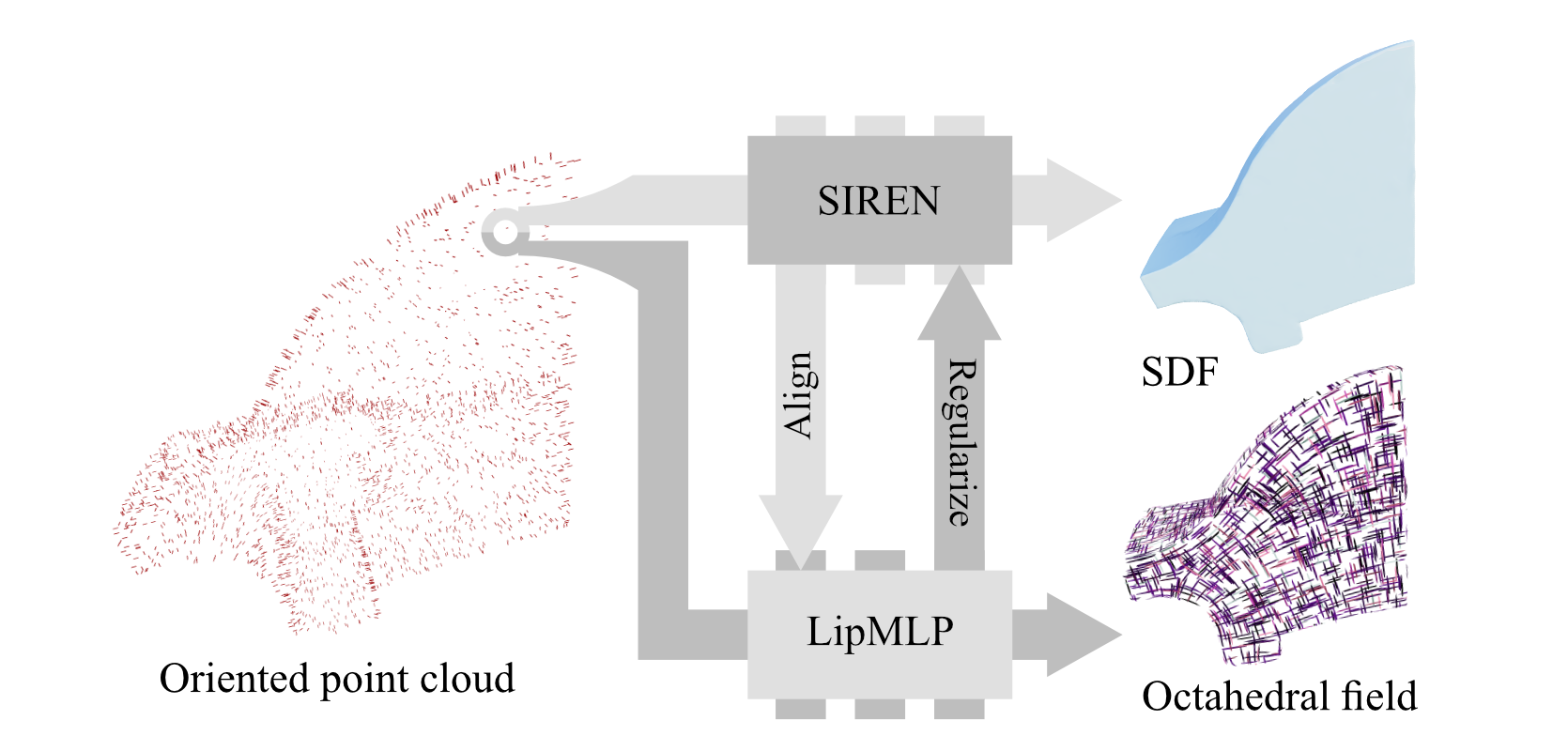
To fit SDF, we use Siren and follow its common practice. The octahedral field, on the other hand, is supervised to match the orientation of point samples, while elsewhere regularized to be locally as smooth as possible. To encourage smoothness, instead of minimizing gradient norm, we directly leverages LipMLP, that speeds up training by 50%.

Key results​

Direct cross field evaluation​

When evaluated on the extracted surface, our implicit octahedral field gives flowlines similar to ones solved globally using FEM, saving the cost of the corresponding step in quadrilateral remeshing.

Extrinsically Smooth Direction Fields by Huang et al.

Practical 3D frame field generation by Ray et al.

Octahedral Frames for Feature-Aligned Cross Fields* by Zhang et al.

Ours

* with p=2,ϵ=0p=2, \epsilon=0

Here are some quad meshes generated using MIQ and libQEx from direct MC output of resolution 64364^3

Octahedral prior for surface regularization​

This demo uses GT normals. However, our method works for PCA normals, or without normals if pairing with DiGS or NSH

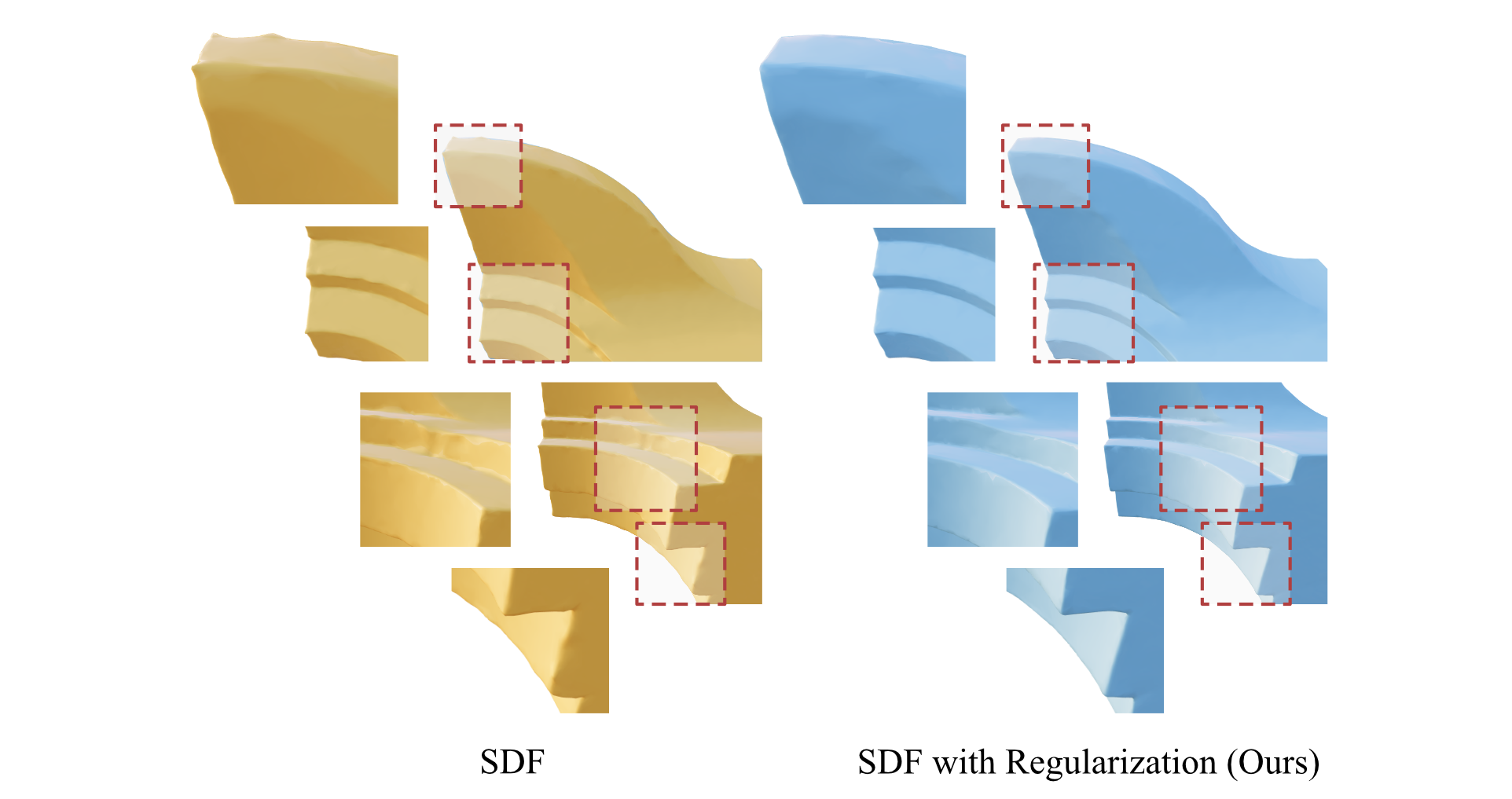
Moreover, the normal aligned octahedral frame in-between supervised samples converges to either π/2\pi / 2 or π\pi at infinitesimal, introducing sharp edge prior to SDF.

Large angle θθθϕϕSmall angle ϕ

Specifically, we regularize the gradient of SDF to match any one axis of the octahedral frame. Here is a toy example to demonstrate the idea



The regularization shines the most for geometry with sharp features. In the following example, we surpass the baseline with a cleaner and sharper reconstruction, only using 1/41/4 of the input samples.

Note: For rendering efficiency, all MC output were simplified with quadratic edge collapsing provided by MeshLab to around 20000 faces (or 60000 for ones with multilayer artifacts).

Neural inverse volume parameterization​

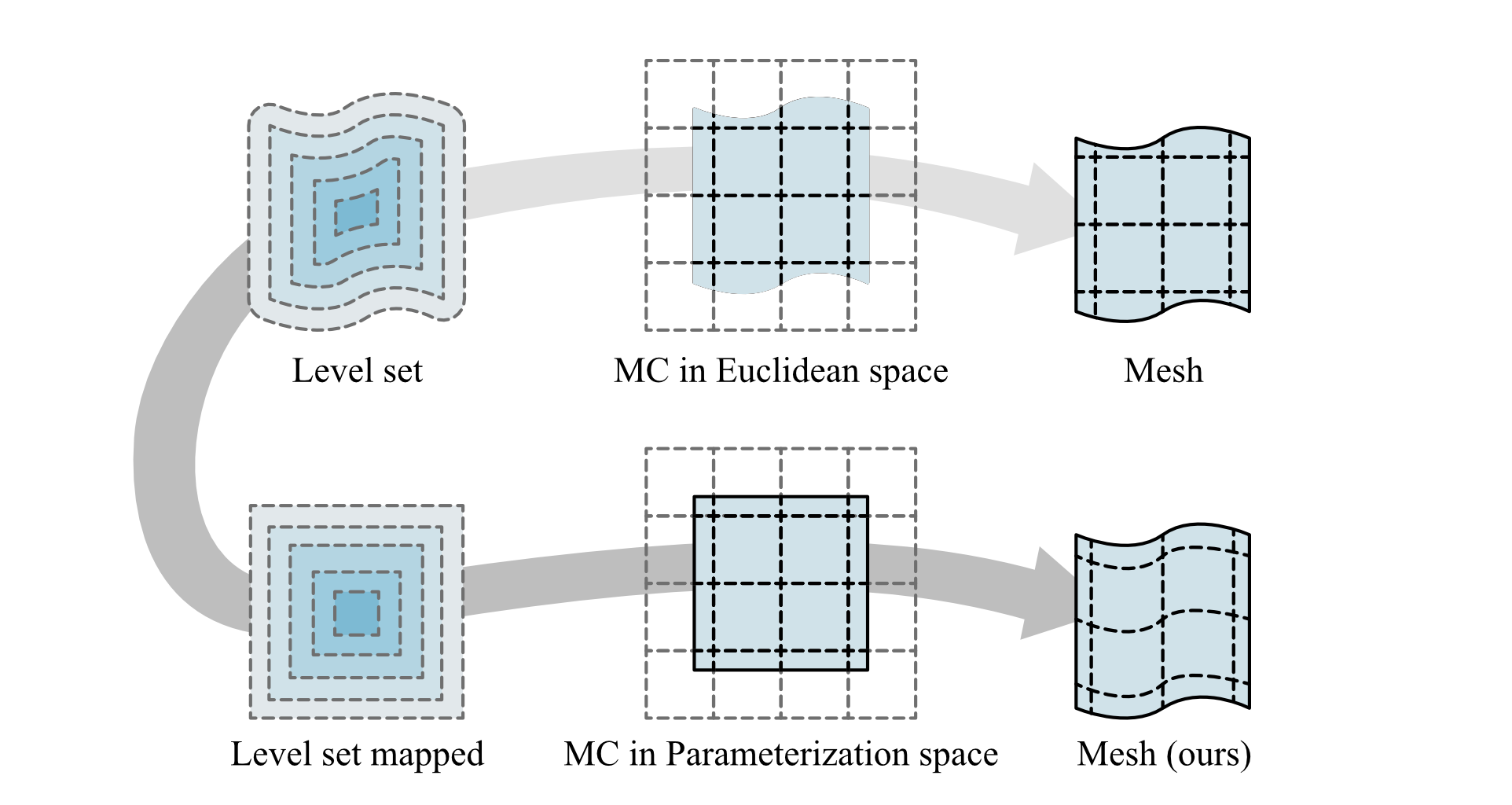
The octahedral field originated in guiding the volume parameterization for the hexahedral mesh generation. As hinted in CubeCover, the hexahedral tessellation of the 3D volume is equivalent to a regular cube tessellation in its parameterization space. Given we fit the implicit octahedral field to align with the zero level set, applying MC in the volume parameterization space should cut the cubes in parallel along their faces, resulting in quad dominant mesh in original space.

In this case, we are interested in CubeCover without integer grid constrains, or namely, the continuous seamless parameterization.

∫V∥∇f−X∥F2 dV\int_{V} \| \nabla f- X \|_F^2 \ d{V}

where f:V∈R3→Vparamf: V \in \mathbb{R}^3 \to V_{param}

But before continue, it is crucial to firstly examine the singularity graph. We follow CubeCover to visualize it as the edges of the bounding tetrahedral mesh.

Our implicit octahedral field gives mostly nested singularity graph that are hard to process. Upon further consideration, even if we successfully cut the singularities and compute inversion-free parameterization, it is still difficult to sample a voxel of coordinates in parameterization space and wrap them back to R3\mathbb{R}^3 to query SDF.

Note that the interior frames are under constrained as its discrete counterpart. We unfortunately could not improve the integrability of octahedral field

Therefore, we take a step back by relaxing the problem to the singularity-free case, and tackle the parameterization inversely using a neural field.

∫Vparam∥∇f−1−(X∘f−1)T∥F2 dVparam\int_{V_{param}} \| \nabla f^{-1} - (X \circ f^{-1})^T \|_F^2 \ d{V_{param}}

where f−1:Vparam→V∈R3f^{-1}: V_{param} \to V \in \mathbb{R}^3

Specifically, we model the inverse parameterization function f−1f^{-1} as a vector potential, and supervise its gradient to match the transpose of octahedral frame (Inverse Function Theorem).

Here is an example for a singularity-free octahedral field.

Extraction in parameterization space

Extraction in original space



Here is an example for an octahedral field with singularities outside the geometry.

Extraction in parameterization space

Extraction in original space



Note: We use Dual Contouring implemented in Libigl

Bonus​

My initial plan was to tackle the volume parameterization with singularity on a tetrahedral mesh, but later realized the problem is much more involved than anticipated (singularity curve is difficult to cut, the parameterization has overlaps, etc.). Nevertheless, it was a fun experience, so I record my attempt here.

Octahedral field

Seam

Parameterization

Acknowledgement​

Our work is largely inspired by the following literature (unordered)

We thank the python community, especially the following softwares that our work relies heavily upon (unordered)