Badge Generation using Polygon Offset
This is a mesh generation project that I worked on in industry. The goal is straightforward: given a cover image, generate a badge-like textured 3D model, with its edge bevel customizable by artists.

Pipeline using my fan art of Britz as cover image
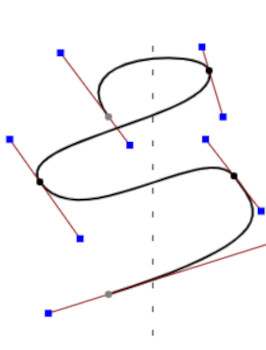
In the initial assessment, the edge can be customized with a curve editor, and the generation is a perfect use case for Blender bevel modifier. However, the latter introduces self-intersections that are nontrivial to resolve--the only solution I found is to tetrahedralize everything and then filter using generalized winding number, but my early attempt failed due to the crash of TetGen.

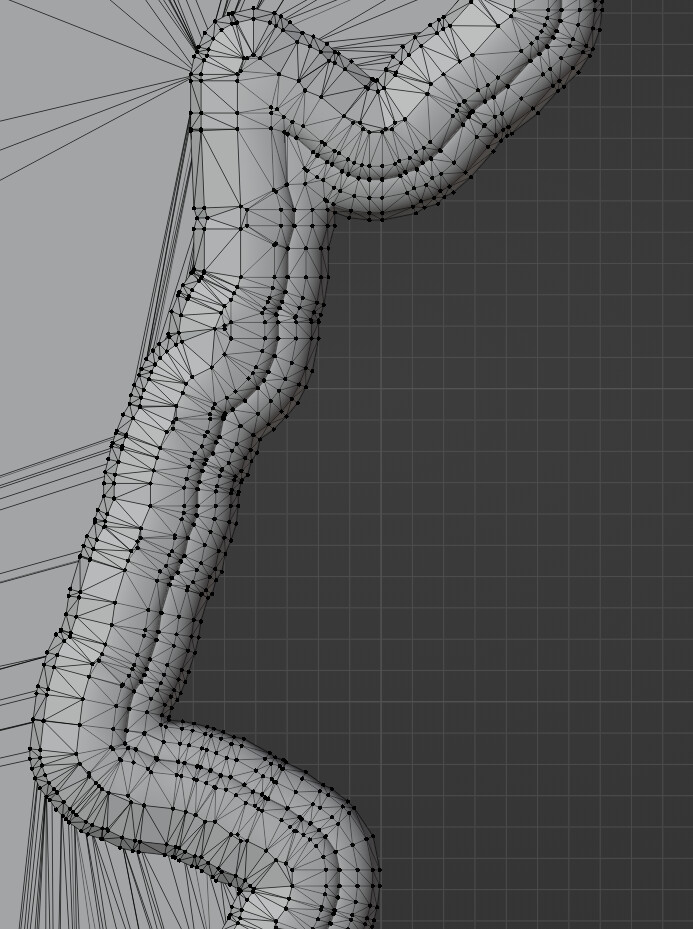
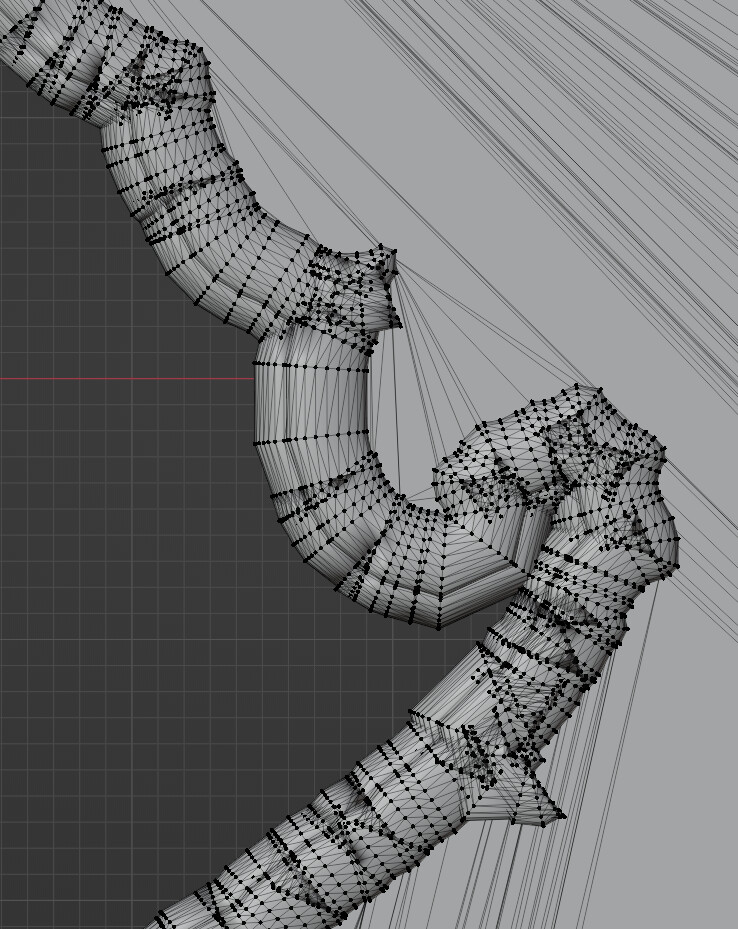
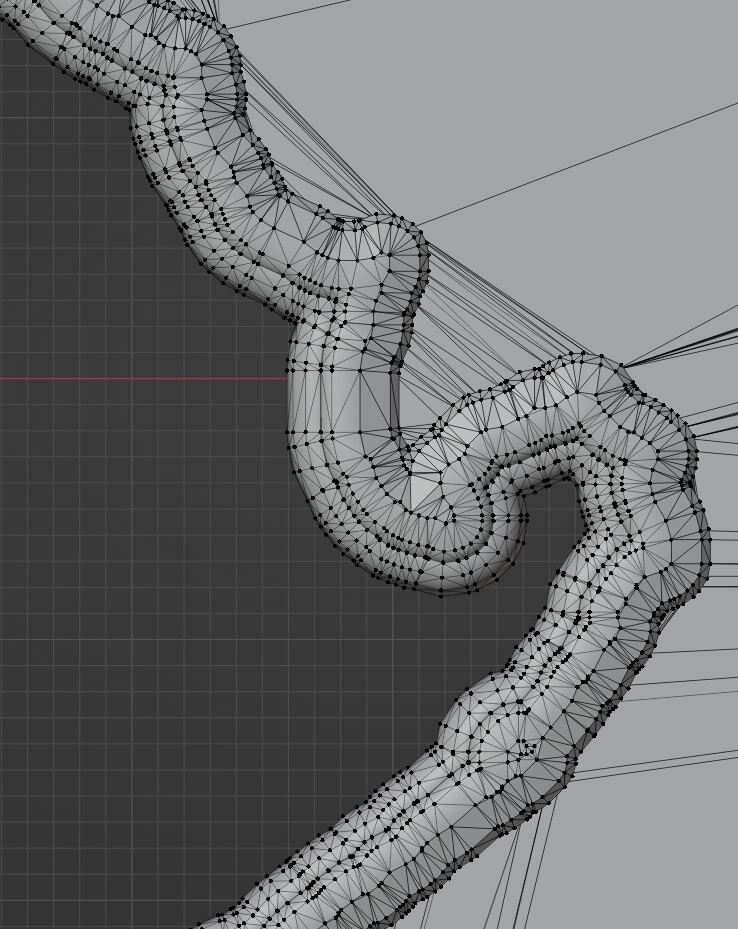
Blender bevel
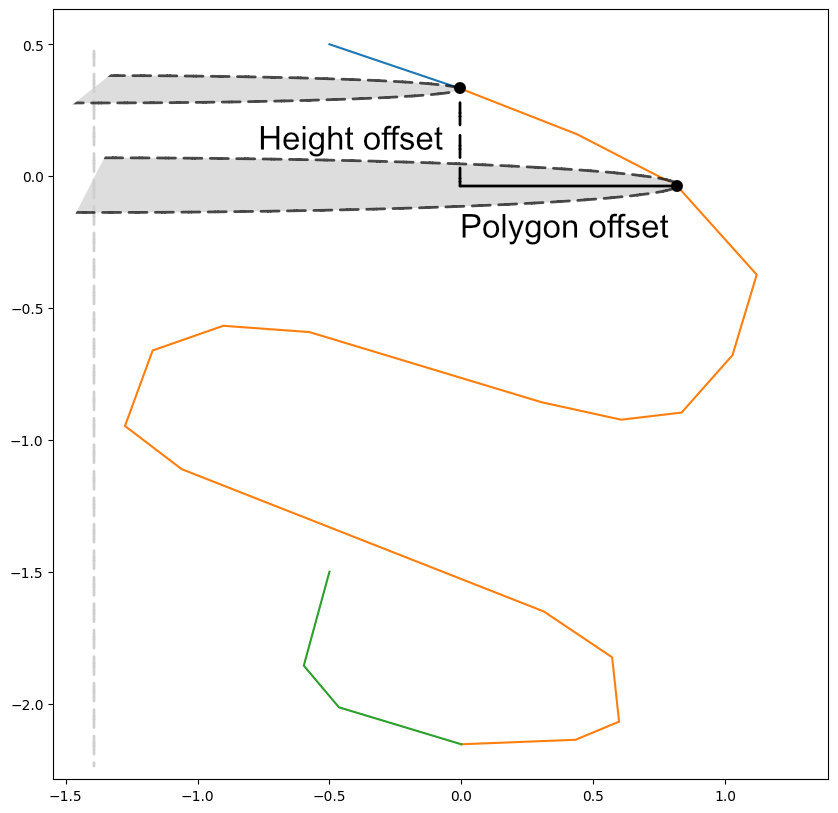
Polygon offset
After observing a sample model made by our 3D artist, I was immediately intrigued--it is mostly quad, with boundary aligned edge loops beautifully propagating towards middle like ripples. He specifically emphasized the importance of the placement of those edge loops, so I decided to mimic it by the follow steps:
- Split edge bevel curve as segments, with its horizontal projection as offset distance
- Extract boundary polygons of input image
- Offset these polygons consecutively as contour map
- Tessellate each pairs of adjacent polygons
- Use Blender to perform the rest (remove duplicated vertices, assign UV coordinates and textures, etc.)
Curve split
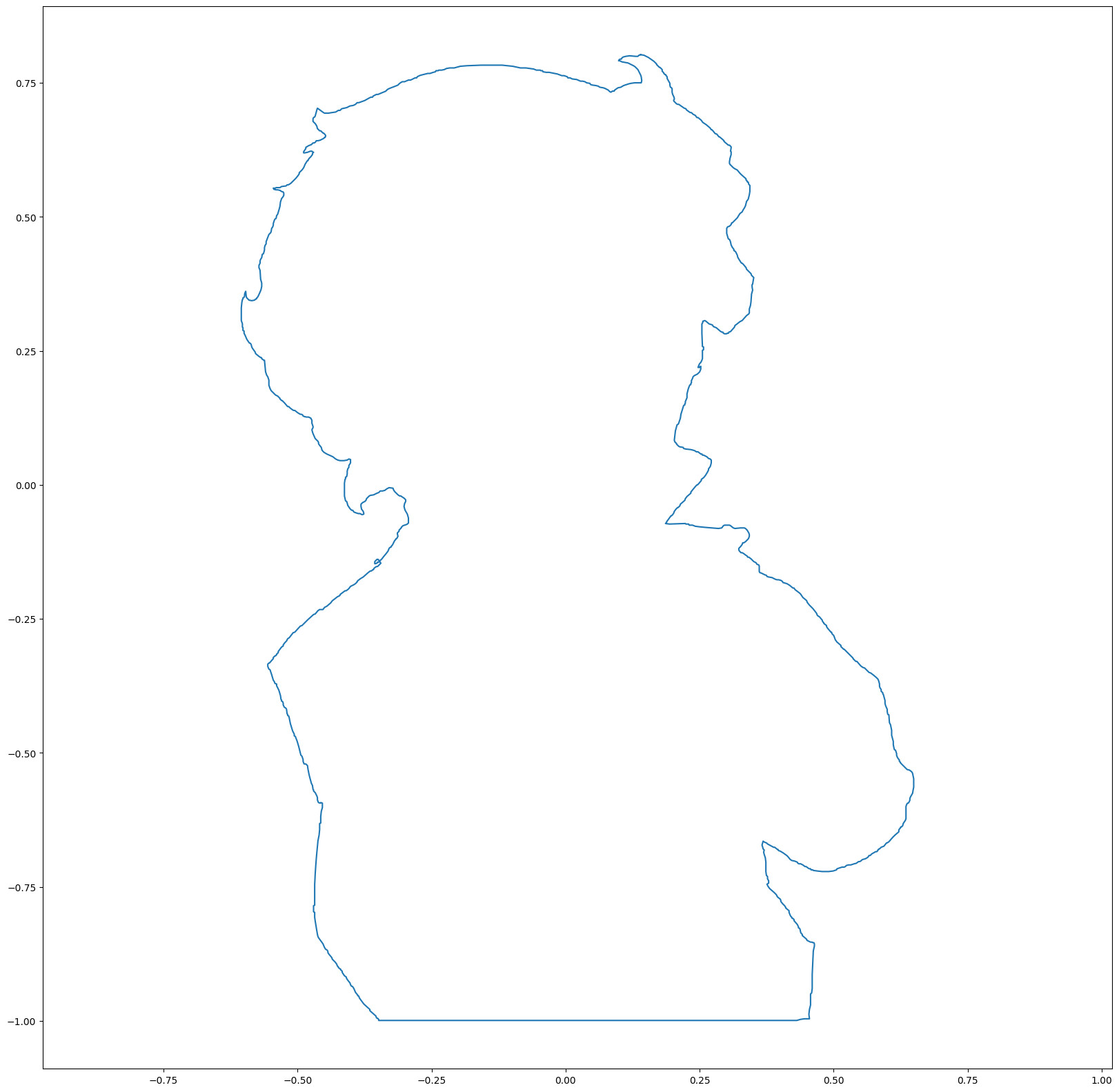
Boundary extraction
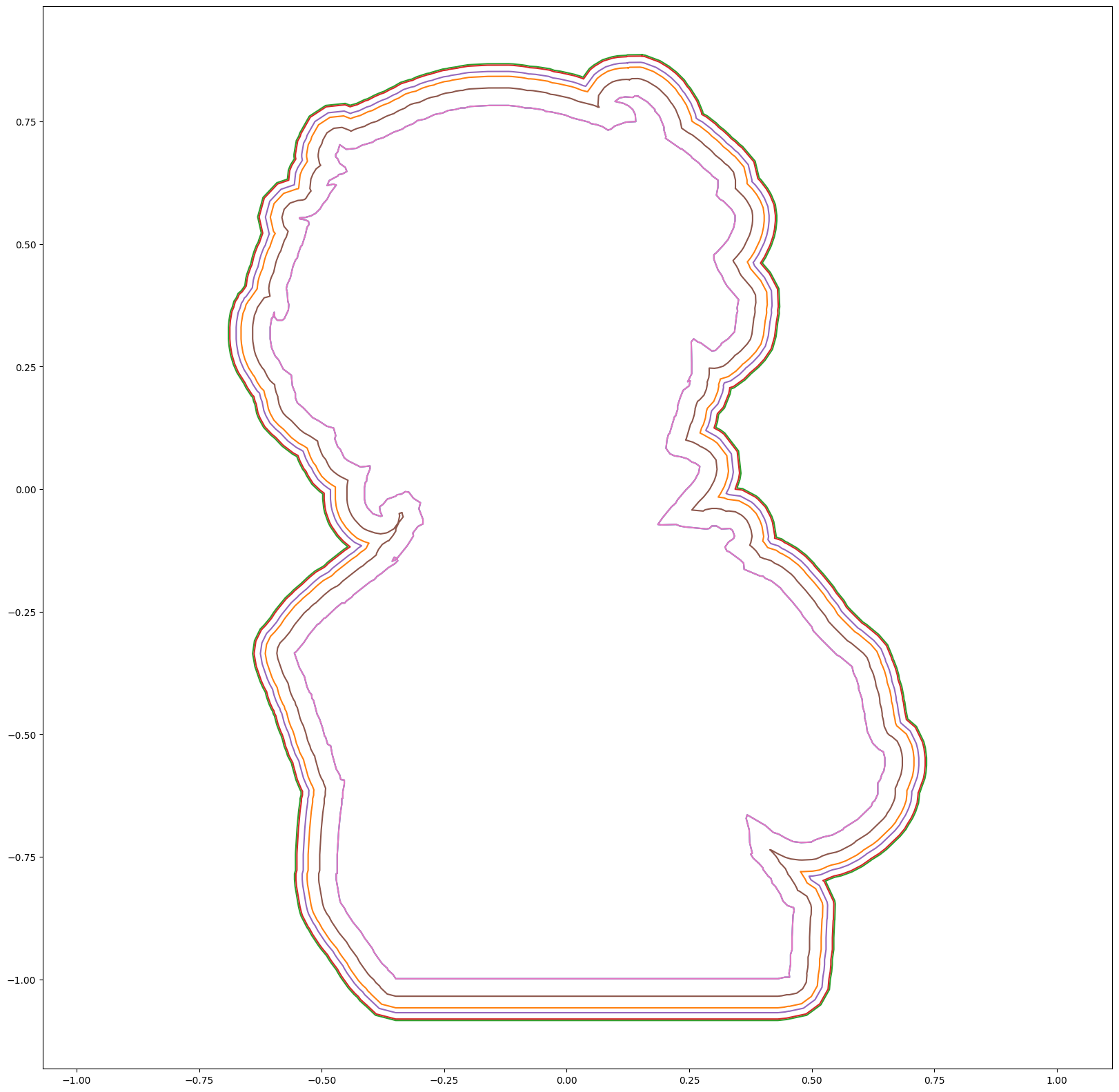
Polygon offset
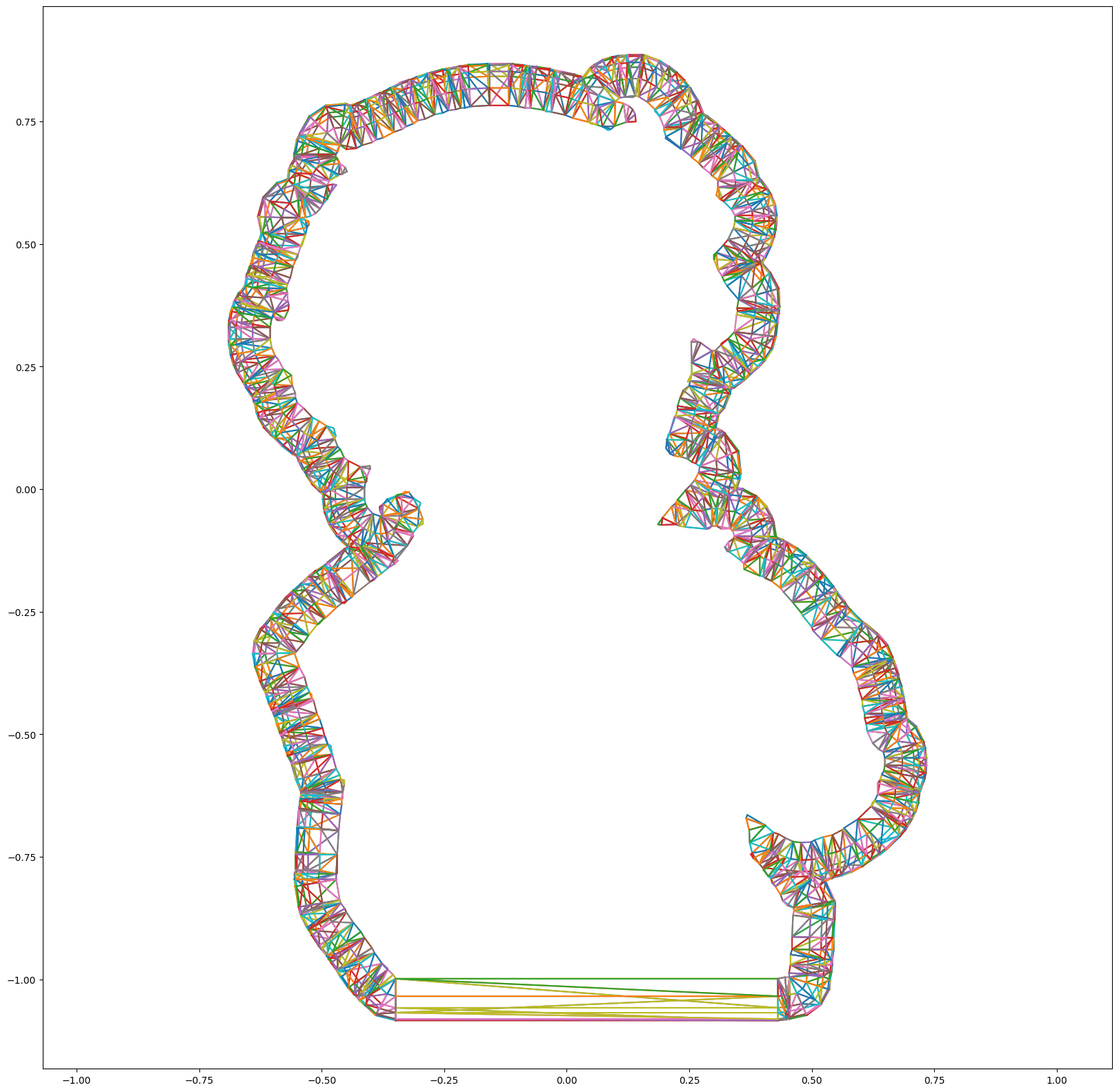
Tessellation
Afterthoughts Though the proposed method is robust, reasonably fast (around 3 seconds) and can produce meaningful edge loops, it regrettably gives triangle mesh that cannot completely fulfill the artists' needs. Nevertheless, it is the project that brought me in and captivated me in geometry processing.
Polygon Offset
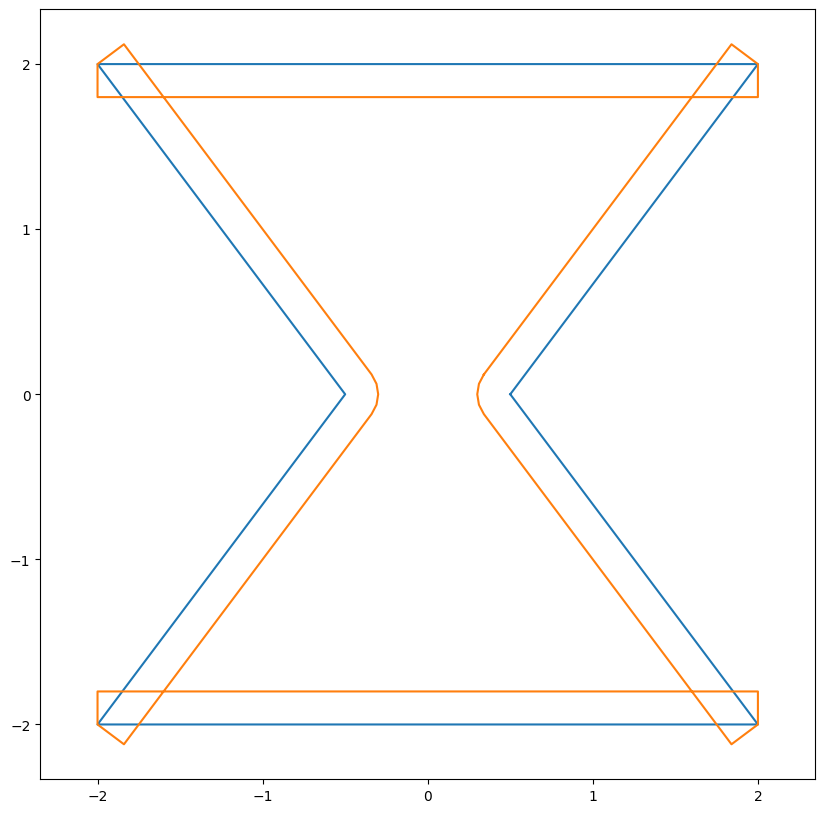
The initial step is to offset boundary polygons, that I implemented the algorithm proposed by Chen et al.. It first translates polygon edges in normal direction by user specified distance. For concave vertices, connect ends of offset edges by arcs. For convex vertices, connect offset ones with this shared vertices. The winding number (implemented in GLU) can then be applied to filter out closed loops.
Toy example 1:
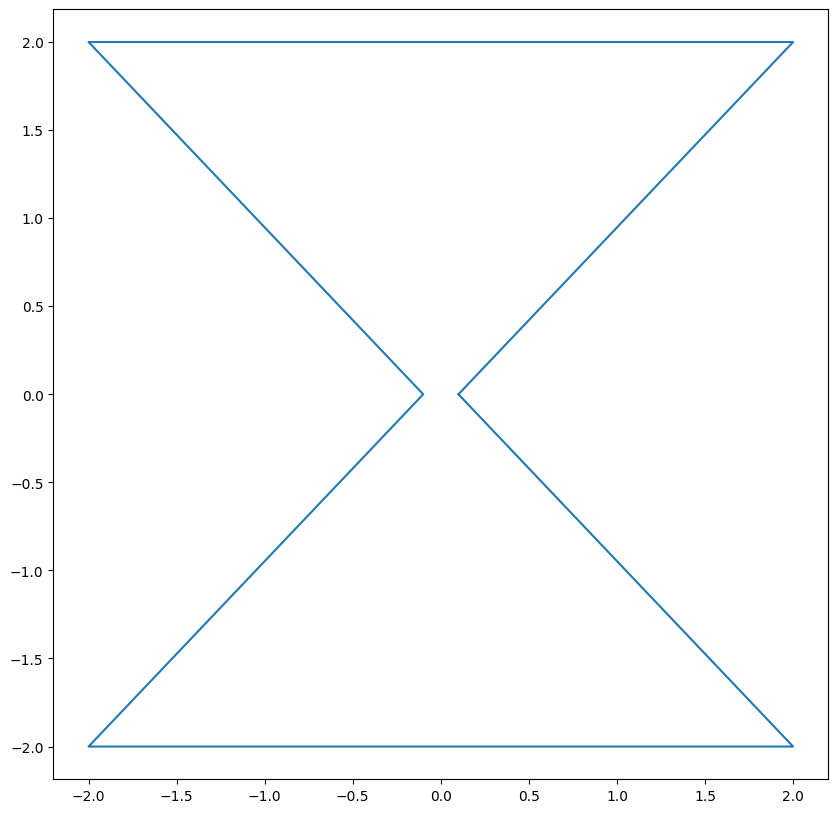
Polygon
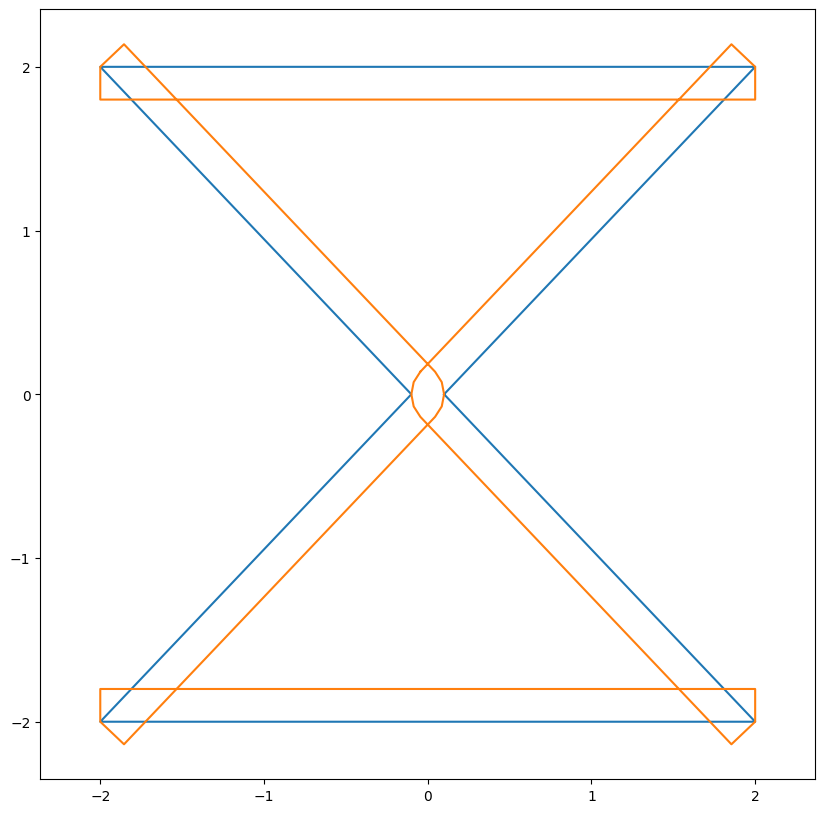
Offset
Cleanup
Toy example 2:
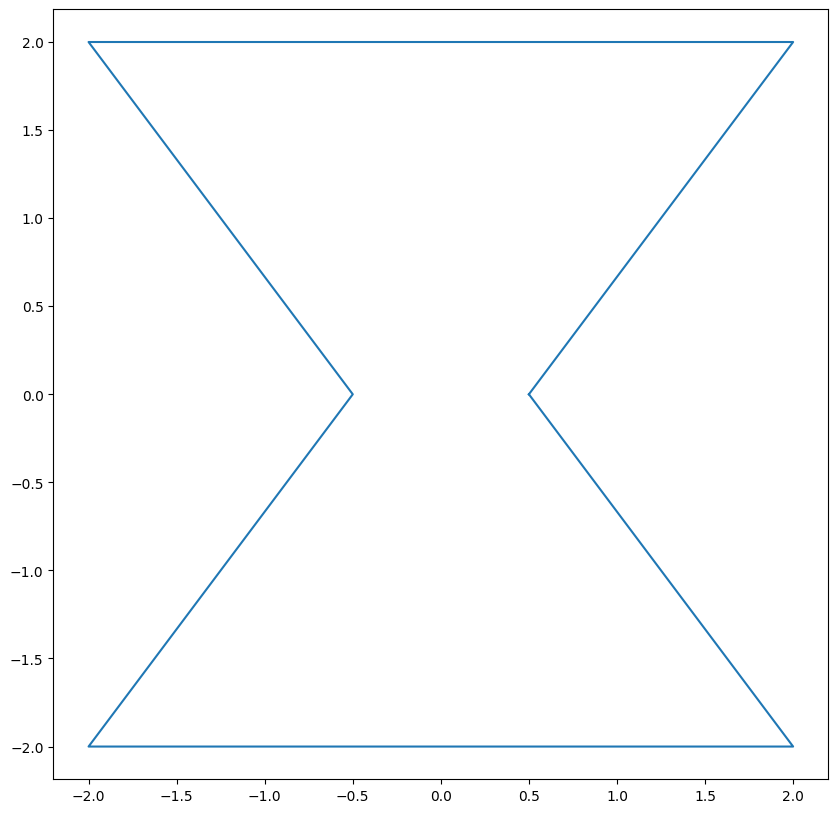
Polygon
Offset
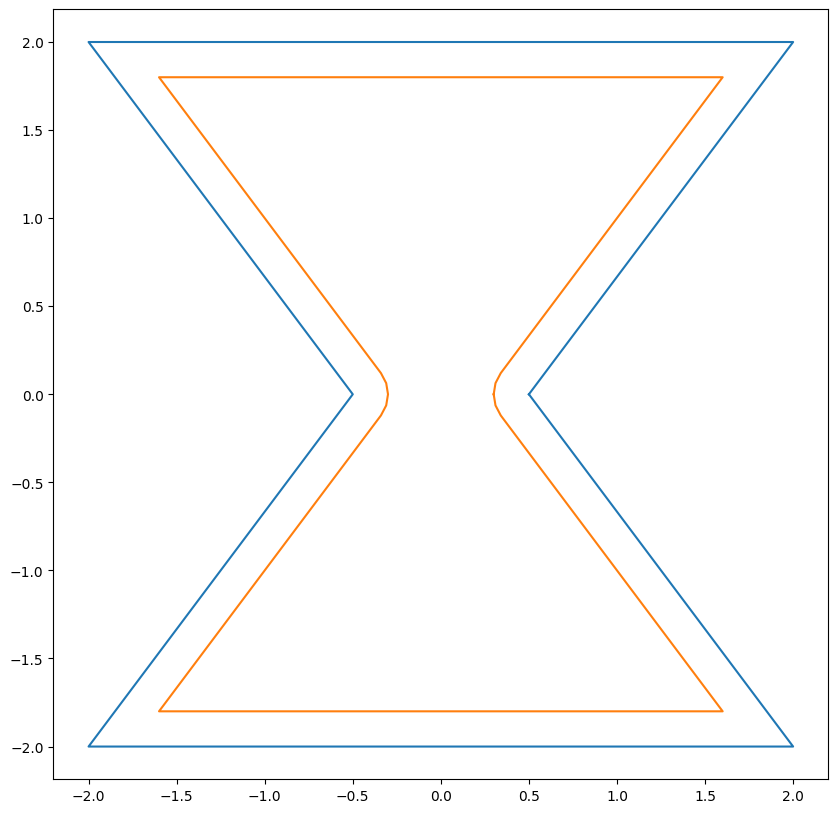
Cleanup
Tessellation
To tessellate the gap between offset polygons, the naive approach is to 2D tessellation methods, such as line sweeping. However, since the inner and outer polygons require to be offset by height displacements, the resulting tessellation causes substantial artifacts when lifted in 3D. Simply connect closest vertices is prone to self-intersection due to potential topology change. One feasible solution I found is to use Delaunay triangulation.
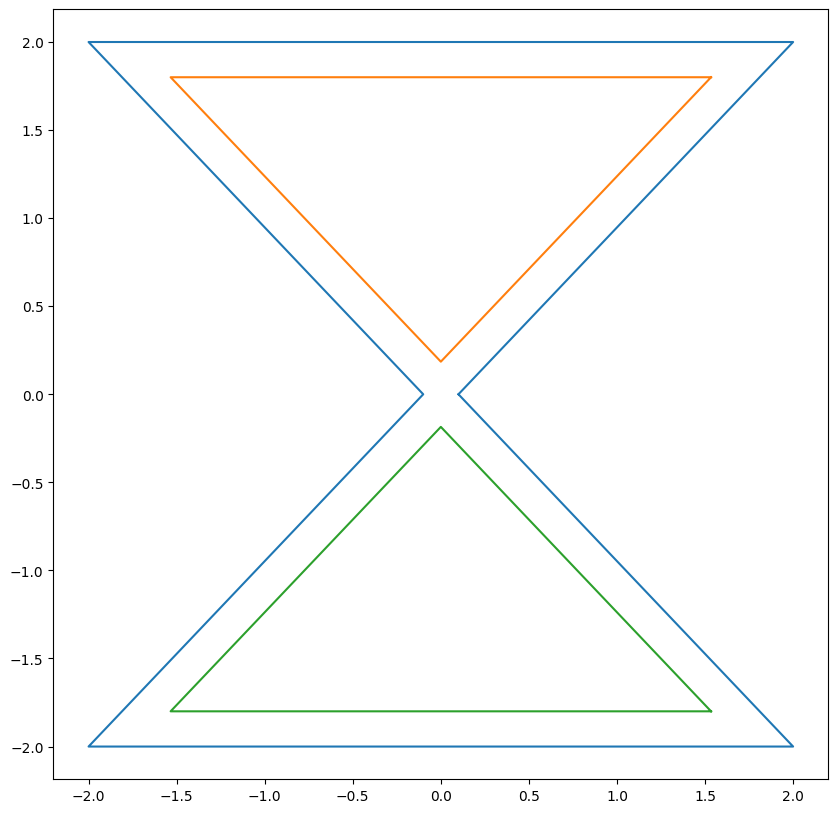
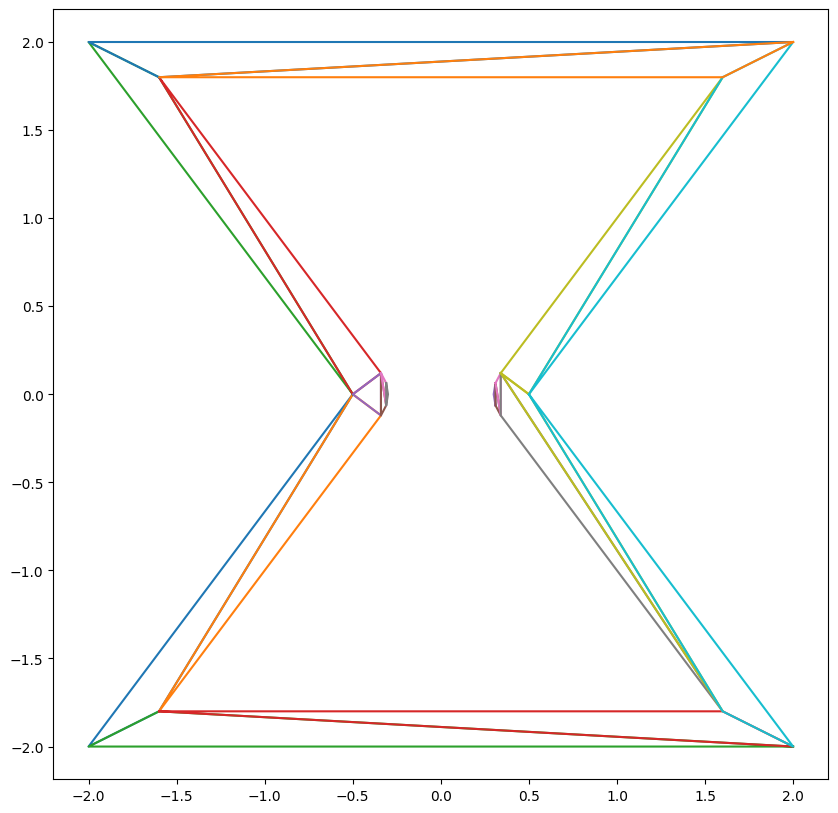
Toy example 1:
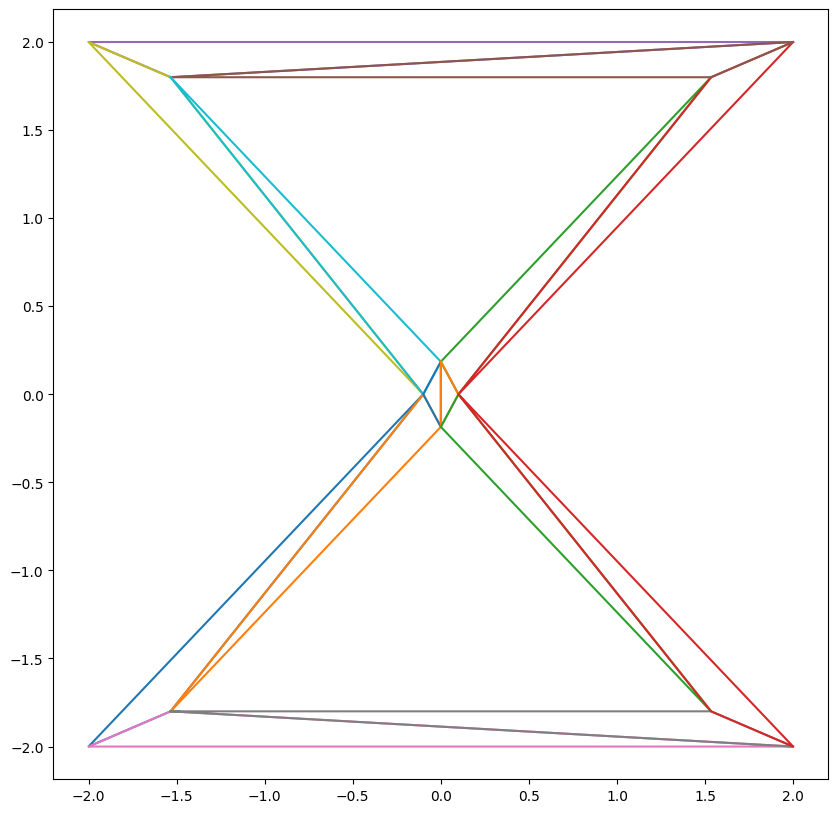
GLU
Delaunay
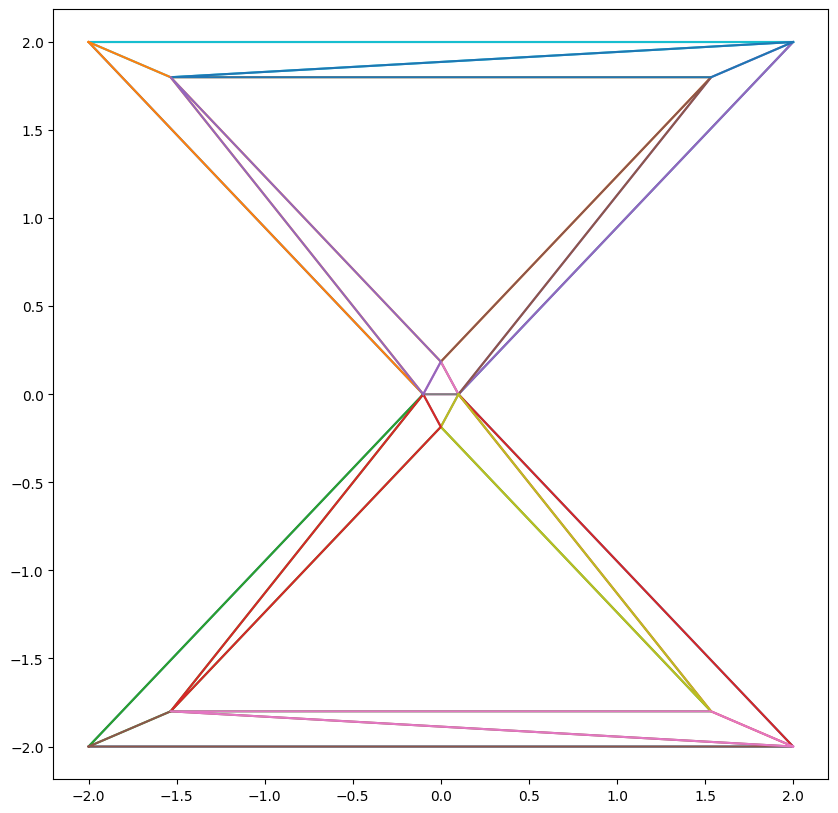
Toy example 2:
GLU
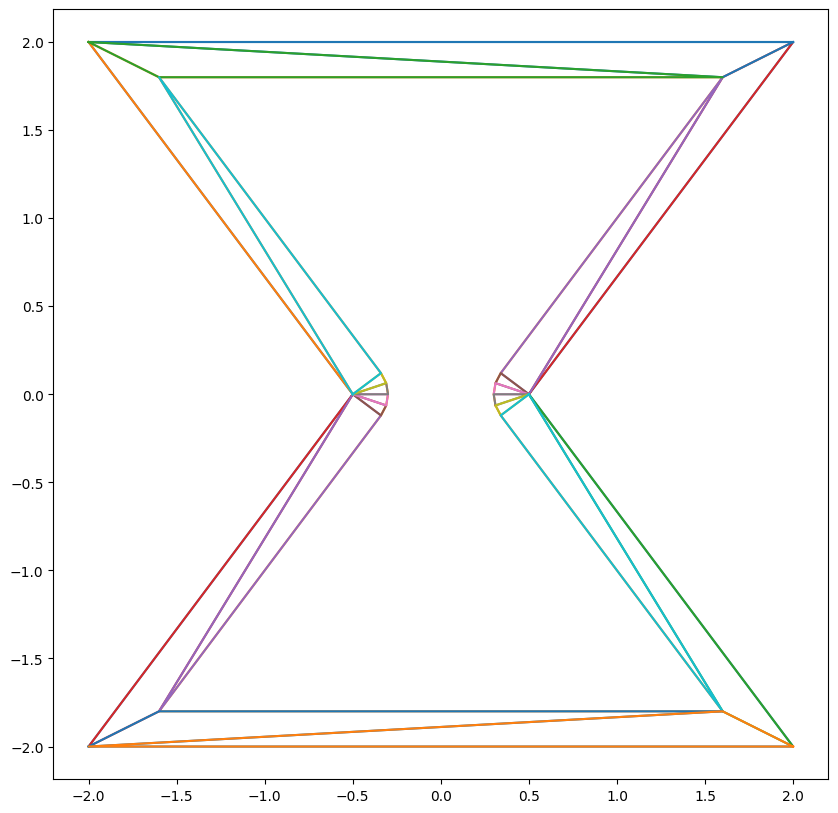
Delaunay
Notice how Delaunay triangulation automatically handles topology change
Practical concern
Since the triangulation produces a convex hull, I filtered out simplices with their barycenters outside the gap, as well as edges that intersect exterior / interior polygons, resulting a soup of edges. The recovery of simplices is the problem of finding all chordless cycles in undirected graph, which can be solved using wall-walking algorithm, by marking the directed edge traversal (boundary once, elsewhere twice).

Delaunay triangulation
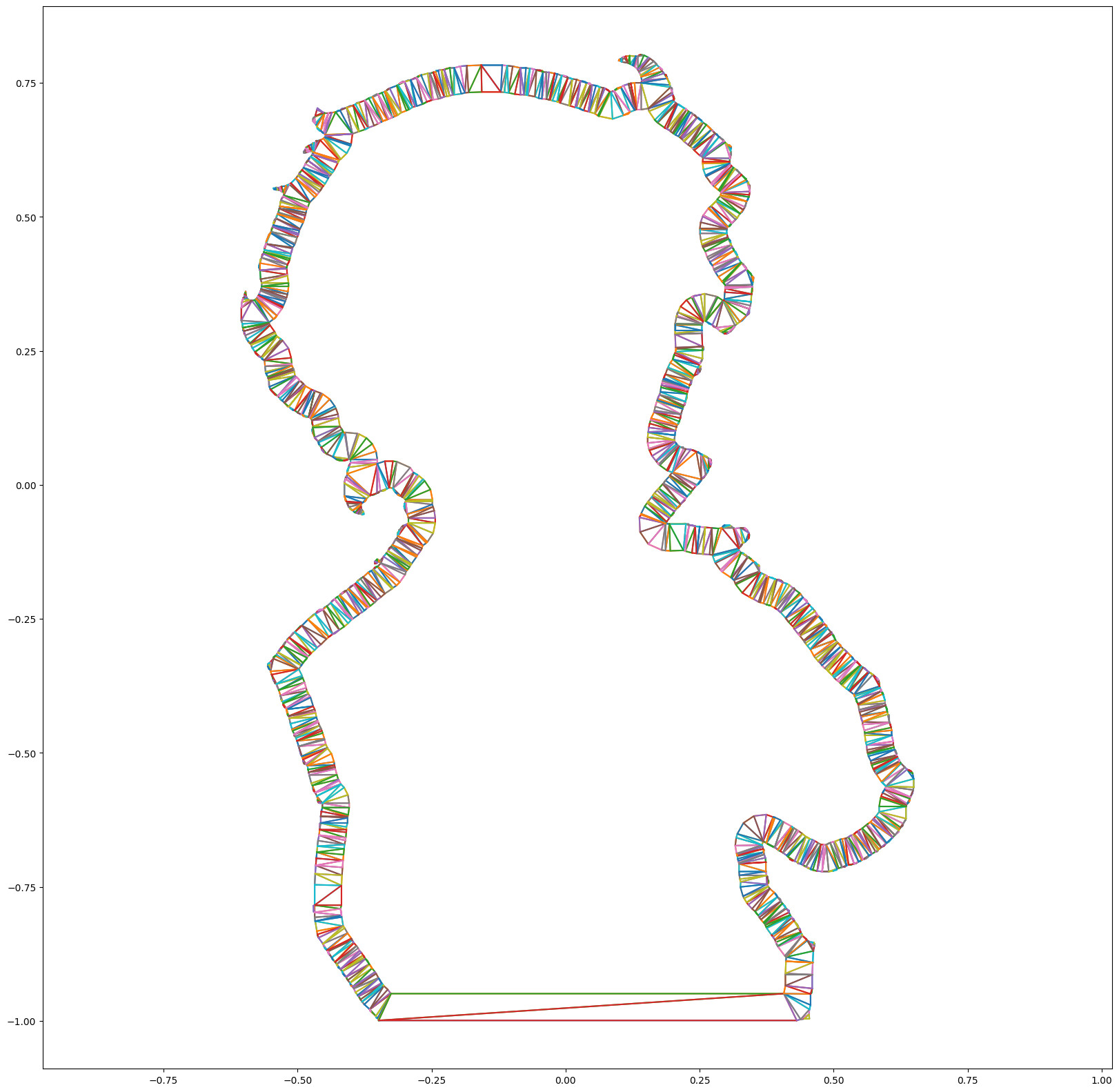
Triangulation cleanup
Afterthoughts The edge filtering could be significantly simplified using half-edge data structure and BFS. In fact, it won't even be necessary if I use constrained Delaunay triangulation, such as Triangle
Limitations
Delaunay triangulation is angle dependent. Notice how the central edge gets flipped as dihedral angle gets small, resulting undesirable artifacts

Delaunay
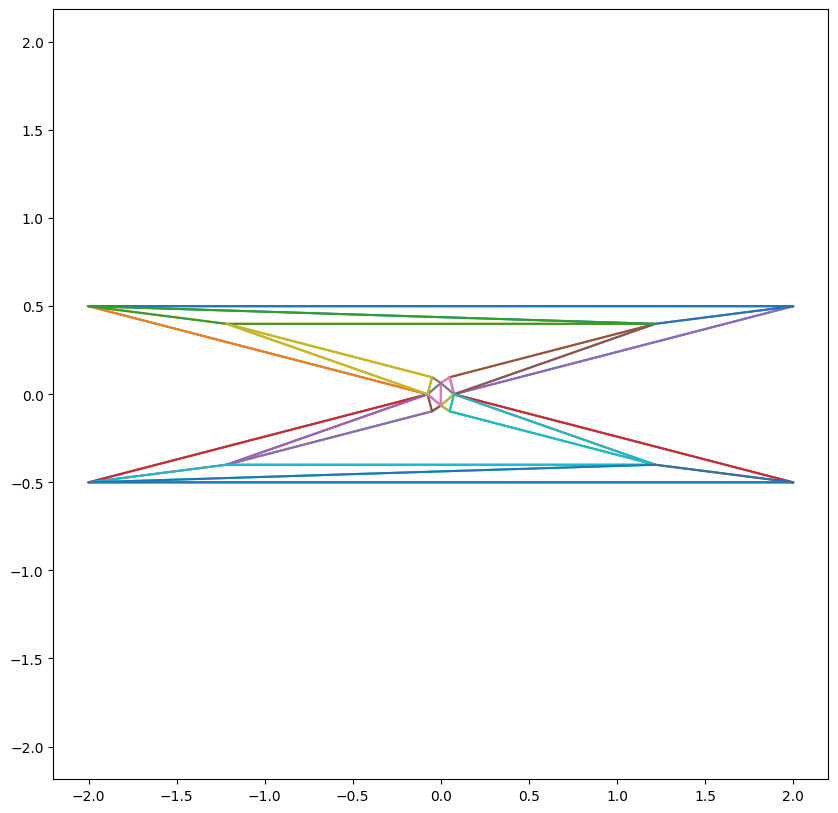
Delaunay